История зототого сечения
История золотого сечения интересна и увлекательна. Она еще раз подтверждает, что тайны природы скрыты и ревниво ею охраняются. Тайна золотого сечения — не исключение.
В 1911 г. французский художник Анри Матисс (1869 — 1954) посетил Россию. В Москве он увидел старинные русские иконы. «Русские и не подозревают, какими художественными богатствами они владеют... Ваша учащаяся молодежь имеет здесь, у себя дома, несравненно лучшие образцы искусства..., чем за границей. Французские художники должны ездить учиться в Россию: Италия в этой области дает меньше», — писал художник позже 1.
Много лет спустя Матисс вспоминал, как «тронуло» его древнерусское искусство и какое воздействие оказало на его творчество: «Ему предаешься тем сильнее, чем яснее видишь, что его достижения подкреплены традицией — традицией древней» 2. Матисс, несомненно, имел в виду традиции искусства Греции классической поры. Он увидел, что Русь через Византию унаследовала живую традицию античного искусства и в своих исторических и национальных условиях продолжала ее. Пока Италия возрождала античность, пытаясь из обломков и развалин составить цельное представление о древности, искусство живописи и архитектуры на Руси достигло больших высот.
Приехав в Советский Союз, американский художник Антон Рефрежье восторженно воспринимает сохранившиеся росписи, выполненные древнерусскими художниками. «Я смотрю на величественные росписи древнерусских храмов, и меня снова и снова потрясает глубина гуманизма искусства, которое поднялось над церковной догмой до уровня выражения эмоционального духа народа. И я с изумлением смотрю на построение композиции, на пропорции фризов на стенах. Здесь также мы можем учиться знанию закона динамической симметрии, абсолютной вере художников в эти законы, раскрытые древними греками и подтвержденные во все великие периоды архитектуры и живописи», — писал он в статье «На языке, понятном массам», опубликованной в газете «Советская культура» 21мая 1974 г. В той же статье Антон Рефрежье отмечает достоинства творений художников эпохи Возрождения: «Я бы назвал два таких качества — глубокий гуманизм (это содержание) и ответственное, уважительное отношение к специфике настенной живописи, знание геометрии, динамической симметрии, правил «золотой середины» (это форма) ...Художник, не будучи осведомленным в геометрии, в законе динамической симметрии, самое большее, что может сделать, это расположить все в определенном порядке, иначе — создать коллаж». Такая высокая оценка золотого сечения и его проявления в русском искусстве, безусловно, побуждает нас к изучению этого феномена.
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н. э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамоиа свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления. Ранее уже упоминалась плита фараона Нармера (рис. 22), построенная в пропорциях золотого деления.
Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников (рис. 23, а).
Платон (427 — 347 гг. до н. э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления (рис. 23, б).

Рис. 23. Динамические прямоугольники (а) и античный циркуль золотого сечения (б)
В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н. э.), Папп (III в. н. э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В историю золотого сечения косвенным образом вплетено имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г. вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила: «Сколько пар кроликов в один год от одной пары родится?» Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:
| Месяцы | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | и т.д. |
| Пары кроликов | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | и т.д. |
Ряд цифр 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д. стал известен в наука как ряд Фибоначчи. Его особенность состоит в том, что каждый его член, начиная с третьего, равен сумме двух предыдущих: 2 + 3=5; 3+5 = 8; 5 + 8=13; 8+13 = 21; 13+21 = 34 и т. д., а отношение чисел ряда все больше и больше приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34:55 = 0,618. Это отношение обозначается символом Ф. Только это отношение — 0,618:0,382 — дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему. Ряд Фибоначчи мог бы остаться только математическим казусом (случаем), если бы не то обстоятельство, что все исследователи золотого деления в растительном мире, а также и в животном, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре. Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его называют творцом начертательной геометрии.
Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г. по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. Они стали друзьями. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства: бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок — бога отца, а весь отрезок — бога духа святого). На золотую пропорцию был наброшен мистический покров.
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится в науке до сих пор как самое популярное.
Характерно, что в то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет: «...Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать» 3.
Дюрер сетует, что секреты древних утеряны, что отцы церкви не должны так яростно уничтожать все, что осталось от древних. Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица — ртом и т. д. Известен пропорциональный циркуль Дюрера.
Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).
В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь «открыто» золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».
Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа — важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8=1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8:5=1,6. У новорожденного пропорция составляет отношение 1:1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела — длина плеча, предплечья и кисти, кисти и пальцев и т. д.
Верность своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону. Следующая его книга имела название «Золотое деление как основной морфологический закон в природе и искусстве». В 1876 г. в России была издана небольшая книжка, почти брошюра, с изложением этого труда Цейзинга. Автор укрылся под инициалами Ю. Ф. В. Характерно, что в этом издании не упомянуто ни одно произведение живописи.
В конце XIX — начале XX вв. появилось немало чисто формалистических теорий о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т. д.
Анархия капиталистического производства привела в XX в. к тому, что продукция, изготовленная одним предприятием, сильно отличалась от аналогичной продукции других предприятий. При перевозке такой продукции нередко оказывалось, что она не соответствует размерам транспортных средств. Такое же положение наблюдалось и в строительном деле.
Французский архитектор Ле Корбюзье (1887 — 1965) разрабатывает единую систему величин. За основу был взят средний рост человека, равный 175 см. Была построена шкала золотого сечения, которая и дала необходимые размеры. Эту шкалу Ле Корбюзье назвал модулором. Пользуясь своим «модулором», Ле Корбюзье строил отдельные здания и целые комплексы сооружений.
На девятой выставке «Триеннале» в Милане в 1951 г. три дня были посвящены золотому сечению. В эти дни было проведено первое международное совещание на тему пропорций в искусстве, а выставка «Триеннале» 1954 г. была полностью посвящена «божественной пропорции» и явилась восхвалением золотого сечения — «древнейшей тропы человечества, указанной Пифагором» (Ле Корбюзье). К сожалению, речь там шла в основном об архитектуре.
Следует упомянуть заслуги Г. Б. Борисовского. В книге «Наука. Техника. Искусство» (М., 1969) автор отдает должное золотому сечению, но указывает на его слабую сторону: золотое сечение характеризует только количественные отношения. Он приводит слова Жолтовского о колбасе (сказанные в шутку), что если разрезать тухлую колбасу в золотом сечении, то она не станет вкуснее. Отношения, свойственные золотой пропорции, выраженные арифметически или геометрически, действительно определяют только количественные отношения. Но эти же отношения, воплотившиеся в живых формах листьев, цветов, животных, доставляют нам эстетическое удовлетворение, радость, мы наслаждаемся красотой формы. Тем более они приятны нам в произведениях рук человеческих: зданиях, статуях, картинах, коврах, вазах и т. д., которые мы пробуем не на вкус, а смотрим на них глазами.
В нашей стране в довоенные годы были изданы книги о золотом сечении в архитектуре: Н. Врунов. Пропорции античной и средневековой архитектуры. — М., 1935; Г. Д. Гримм. Пропорциональность в архитектуре. — Л.; М., 1935. Осуществлялись переводные издания: Г. Е. Тимердинг. Золотое сечение. — М., 1924; М. Гика. Эстетика пропорций в природе и искусстве. — М., 1936; Д. Хэмбидж. Динамическая симметрия в архитектуре. — М., 1936. И в этих книгах проявление закона золотого сечения в живописи не затрагивалось.
В редакционном примечании к книге М. Гика «Эстетика пропорций в природе и искусстве» указывается, что многие ученые, занимавшиеся золотым сечением, не идут дальше простой констатации факта: «Между тем, задача заключается в том, чтобы объяснить его причины. Такую попытку делает советский исследователь Ф. И. Зубарев, работы которого о золотом сечении подготовляются сейчас к печати» 4. Неизвестно, были опубликованы работы Ф. Зубарева или нет.
В послевоенные годы заметно расширение и углубление внимания ученых различных специальностей к проблеме золотого сечения. В 1974 г. И. И. Шафрановский публикует работу «Динамическая симметрия в кристаллографии, минералогии, петрографии и органическом мире» (Записки Ленингр. горн, ин-та им. Г. В. Плеханова. — Т. XII, вып. 2). В 1977 г. напечатана книга А. П. Стахова «Введение в алгоритмическую теорию измерения», а в 1979 г. — его же «Алгоритмическая теория измерения» (М., Знание), в которых изложено применение чисел ряда Фибоначчи и золотой пропорции для улучшения работы аналого-цифровых преобразователей. В 1979 г. И. Шмелев в журнале «Архитектура СССР» публикует статью «Канон. Ритм, пропорция, гармония» (№ 2), в которой излагает дальнейшее развитие идеи «модулора» Ле Корбюзье, что позволило ему раскрыть механизм гармонии ритмических взаимосвязей в пропорциях мужского и женского тела, их динамическую дополнительность по отношению друг к другу, что снимает недоверие к золотому сечению на том основании, что пропорции тела женщины не соответствуют золотым.
Особый интерес представляет статья М. А. Марутаева «О гармонии как закономерности» в сборнике «Принцип симметрии» (М., 1978). Он отмечает, что в современной науке существуют три проблемы: 1) природа золотого сечения, 2) загадка числа 137 и 3) природа приблизительной симметрии, которая относится к живой природе, искусству, а в последнее время и к физике. Далее он показывает, что все три проблемы представляют собой одну проблему: нарушенная симметрия (приблизительная симметрия), число 137 и золотая пропорция взаимосвязаны. Это подтверждает, по мнению автора, фундаментальность принципа золотого сечения и позволяет объяснить многие факты, которые раньше рассматривались как противоречащие принципу золотого сечения.
Болгарский журнал «Отечество» (1983 — № 10) опубликовал статью Цветана Цекова-Карандаша о «втором золотом сечении», которое вытекает из основного сечения и дает новое отношение 44:56. Эта пропорция обнаружена в архитектуре, а также имеет место при построении композиций картин удлиненного горизонтального формата.
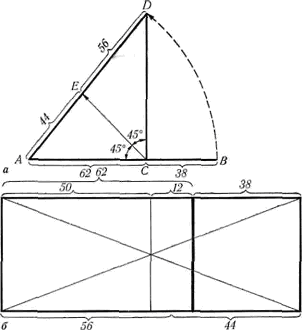
Рис. 24. Второе золотое сечение: а — геометрическое построение; 6 — линия второго золотого сечения на картине
Отрезок АВ делится в пропорции золотого сечения (рис. 24, а). Из точки С восставляется перпендикуляр СД. Радиусом АВ находится точка D, которая соединяется линией с точкой А. Прямой < АСД делится пополам. Из точки С проводитсялиния до пересечения с линией AD. Точка Е делит отрезок AD в отношении 56:44. На рис. 24, б показано нахождение линии второго золотого сечения на картине. Она находится посередине между линией золотого сечения и средней линией картины.
1 Матисс А. Сборник статей о творчестве. — М.,1958. — С. 99.
2 Там же. — С. 104.
3 Дюрер А. Дневники, письма, трактаты. — Л.; М., 1957. — Т. 2.- С. 37,
4 Гика М. Эстетика пропорций в природе и искусстве. — М., 1936. — С. 301.
