Рисунок с натуры
«Современный психолог думает, — писал Н. Н. Волков, — что зрительное восприятие величины и формы, вообще говоря, относительно константно, а для некоторой зоны опыта — почти совсем константно. За психолога говорят, казалось бы, многочисленные факты и строгие экспериментальные наблюдения. Однако за художника говорит длительная практика. Было бы недопустимой близорукостью игнорировать эту практику. Художник действительно видит не константно, или, лучше сказать, умеет видеть не константно».
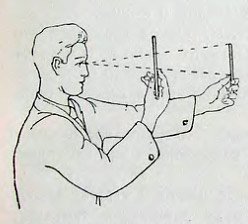
Рисунок 10. Опыт, иллюстрирующий несоответствие перспективной величины предмета «угловому закону»
Справедливо возражая против существования особой «субъективной перспективы», изменчивой и непостоянной, Н. Н. Волков допускает, однако, при этом ошибку, пытаясь доказать полную аналогию между изображением перспективных явлений на рисунке и их передачей путем геометрического построения. Подкрепляя свою мысль о том, что верный перспективный рисунок и точно построенное перспективное изображение должны полностью совпадать в своих формах, Н. Н. Волков ссылается на рассмотренные выше приемы рисования с помощью стекла или сетки, которые применяли живописцы и архитекторы эпохи Возрождения.
«Проекция предмета на плоскость стекла есть, таким образом, — пишет Н. Н. Волков, — с одной стороны, факт восприятия... с другой — классическая задача геометрической теории перспективы… Конечно, художник умеет и привык видеть перспективную величину и форму и без стекла или сетки Альберти. Художнику поэтому трудно согласиться, что законы зрительного восприятия и законы перспективы (геометрической) расходятся. Убеждение, что мы видим именно перспективную величину и форму вещи, глубоко коренится в практике реалистического рисунка».
О чем свидетельствует практика рисунка с натуры, мы увидим в дальнейшем. Здесь же необходимо отметить, что мнение о полном совпадении в довольно значительных пределах законов линейной и наблюдательной перспективы действительно широко распространено как среди современных художников, так и в теоретической литературе по перспективе. В указанном плане этот вопрос трактуется, например, и в последнем издании книги А. П. Барышникова «Перспектива», рекомендованном в качестве учебного пособия для высших художественных учебных заведений. Проблеме соотношения так называемой наблюдательной перспективы с теорией линейной перспективы автор посвящает специальную главу «Теория перспективы и практика наблюдения перспективных явлений при рисовании с натуры». Изложение этой главы А. П. Барышников как раз и начинает с интересующего нас вопроса.
«...Какой вид принимает теория перспективы при рисовании с натуры и надо ли утверждать существование особой наблюдательной перспективы?» — спрашивает автор и отвечает далее на этот вопрос отрицательно:
«Теория перспективы, — пишет он, — не противоречит, а подкрепляет практику рисования с натуры, помогая художнику точнее увидеть своими глазами перспективные явления на всем, что он рисует, и осознать их закономерности, установленные теорией линейной перспективы».
Свою позицию в этом вопросе А. П. Барышников излагает далее приблизительно следующим образом. Если предмет расположен в поле наилучшего зрения, то есть в пределах зрительного угла 28-37°, то его перспективные изображения, полученные путем геометрического построения, совершенно точно передают наши зрительные впечатления. Искажения возникают, по мнению А. П. Барышникова, лишь при нарушении этих пределов.
«В рисунках с натуры художники часто изображают не только то, что действительно находилось в поле зрения, — пишет автор, — но и смежные с тем части пространства... В этих случаях неизбежны перспективные невязки, отступления от правил перспективы или попытки маскировки перспективных невязок».
Приведенные высказывания довольно ясно показывают, как оценивается вопрос о соответствии рисунка и законов перспективы современными психологами и геометрами. В дополнение к этому остается лишь посмотреть, какие практические выводы и рекомендации отсюда вытекают. Поучительным примером в этом отношении может служить ссылка на высказывания авторов книги «Учебный рисунок» — А. М. Соловьева, Г. Б. Смирнова и Е. С. Алексеевой.
