Пример проекции фасада здания
Эти данные и позволяют произвести необходимые построения. На линию горизонта вначале переносятся точки F и M0, затем в точке M0 располагается основание отрезка H — натуральной высоты фасада, взятой в масштабе чертежа. Через вершину отрезка H в точку схода F проводится прямая, которая при пересечении с двумя перпендикулярами, восстановленными в точках A0 и B0, определит перспективные контуры фасада здания.
В тех случаях, когда воспользоваться точкой схода бывает затруднительно, например, при ее расположении за пределами чертежа, можно обратиться к другому приему построения, используя для этой цели боковую проекцию объекта и картинной плоскости.
В данном примере проекцией фасада здания будет являться отрезок H, наложенный перпендикулярно к оси Y на продолжении прямой AB. Искомые отрезки hA и hB также с проектируются в свою натуральную величину, заняв аналогичное положение между осью Y и лучом, проходящим через вершину отрезка H. Причём высоты эти окажутся расположенными на прямых, проходящих через точки A0 и B0 параллельно оси X.
Зная горизонтальную проекцию фасада AB и проекционные размеры высот hA и hB, произвести дальнейшее построение изображения уже не составляет большого труда.
Оба описанных выше способа определения перспективных размеров высот мы будем применять и в дальнейшем при построении более сложных объектов. Первый — при наличии на чертеже точки схода для группы горизонтальных прямых, второй — при ее отсутствии или же при необходимости получения большего числа проекций вертикальных размеров.
Следует сказать также о некоторых приемах перспективного подразделения плоскости фасада в продольном направлении, к которым нам придётся неоднократно обращаться при последующих построениях. Среди этих приемов следует указать, прежде всего, на простейший случай метрического членения фасада с помощью диагоналей, которые всякий раз при пересечении определяют перспективное положение центра прямоугольника, которому они соответствуют (рисунок 53, а). Если же фасад расчленён на нечётное число метрических частей и использовать указанный способ не представляется возможным, то следует обратиться к приему так называемых делительных масштабов.
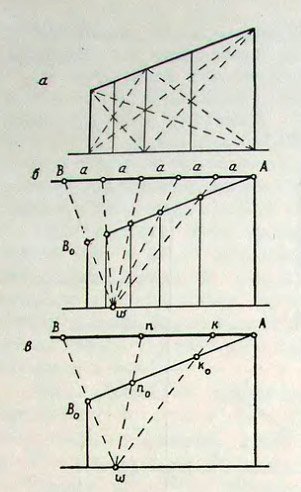
Рисунок 53. Приёмы членения перспективы прямоугольника в заданном отношении
Предположим, например, что нам необходимо разделить фасад здания в продольном направлении на пять равных частей (рисунок 53, б). В этом случае следует провести через вершину ближнего ребра прямую, параллельную линии горизонта и отложить на ней в произвольном масштабе отрезок AB — размер фасада здания, подразделенный на пять равных частей. Соединив далее крайнюю точку отрезка B с вершиной дальнего ребра фасада B0 и продолжив полученную прямую до горизонта, определим положение точки W. В эту точку проведем лучи из всех точек членения отрезка AB, которые и засекут искомое положение этих точек в перспективе.
