Здания и ансамбли
Среди изображений первой группы мы видим ряд картин крупнейших русских мастеров рисунка — М. Н. Воробьева, А. П. Брюллова, В. Д. Поленова, В. В. Верещагина, И. Е. Репина, В. А. Серова, Г. Косякова, а также А. П. Остроумовой-Лебедевой, В. А. Щуко, П. И. Львова и других. При этом нельзя не отметить правдивости приведенных изображений, превосходящих по своим качествам возможности метода перспективных проекций на плоскость, в чем мы убеждаемся при сравнении рисунков с помещенными фотоснимками соответствующих объектов.
Внимательное изучение приведенных изображений показывает, что многие так называемые отклонения от правил линейной перспективы, допущенные рисующими, имеют не случайный или единичный характер, а выступают как закономерное явление, как отражение в рисунках объективных закономерностей зрительного восприятия.
Судить об этом можно по установленному расчетом для каждого из рисунков положению проекционных поверхностей. Эти поверхности в плане, как мы видим на представленных в приложении чертежах, никогда не располагаются перпендикулярно лучу, идущему к центру соответствующего фасада здания. Они всегда отклоняются от подобного положения, уменьшая величину угла, заключенного между плоскостью фасада и картинной поверхностью (смотрите, например, приложение, рисунок 38, 39).
Этой особенностью обусловлен и тог факт, что при изображении на рисунке двух фасадов здания, имеющего форму параллелепипеда, проекционные поверхности, соответствующие каждому из фасадов, пересекаются под некоторым углом. Причем в плане точка их пересечения лежит на луче, идущем к ближнему углу здания (смотрите, например, приложение, рисунок 71).
Если же объект представляет собой более сложную форму, если имеет место чередование нескольких различно расположенных фасадных плоскостей, то соответственно и проекционная поверхность принимает более сложные очертания, причем число образующих ее участков всегда соответствует количеству изображенных плоскостей фасада (смотрите, например, приложение, рисунок 36).

Рисунок 45. Схема приведения отдельных фасадов объекта к параллельному расположению сторон
Отклонение проекционной поверхности от нормального положения по отношению к центральному лучу показывает, что перспективные сокращения, наблюдаемые в натуре и воспроизводимые художником, изменяются не прямо пропорционально увеличению расстояния до объекта, как это принималось в теории линейной перспективы, а в иной последовательности. Причем, чем больше оказываются величины отклонения проекционной поверхности от нормального положения в сторону того иного объекта, тем, следовательно, меньше степень проявления перспективных сокращений на анализируемом изображении.
Отклонения проекционной поверхности от нормального положения, установленные анализом большого числа рисунков с натуры, подтверждают, в частности, необоснованность известного положения проективной геометрии о том, что для установления возникающих искажений картинную плоскость следует располагать перпендикулярно к лучу зрения, идущему в плане к центру предмета.
Следует отметить также еще одну особенность формы полученных проекционных поверхностей. Поверхности эти обычно имеют некоторый изгиб, отражающий перспективное искривление изображенных прямых (см., например, приложение, рисунок 31).
Указанные особенности расположения и формы проекционных поверхностей свое выражение в целом ряде представленных ниже анализов. Однако полученные в результате изучения каждого из приводимых рисунков материалы могли служить лишь приблизительной констатацией обнаруженных закономерностей.
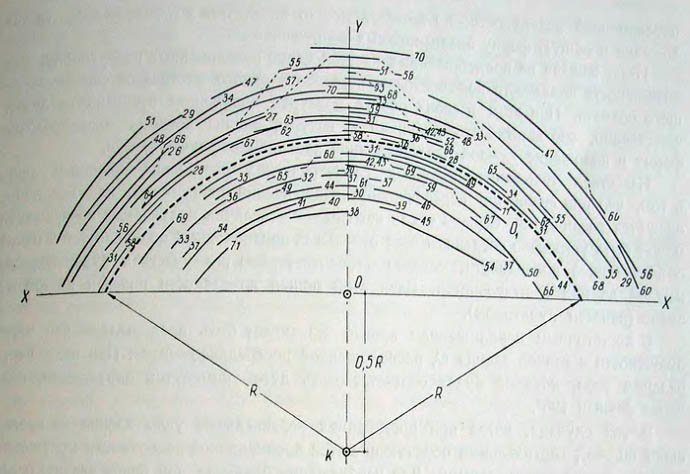
Рисунок 46. Результаты сопоставления проекционных поверхностей в плане для фасадов объектов, расположенных параллельно оси X. Толстой штриховой линией намечено среднее рекомендуемое положение проекционной поверхности
Для получения более конкретных выводов, отражающих не только общую тенденцию проявляющихся закономерностей, но и их количественное выражение, требовалось произвести последовательное сопоставление данных анализа, характеризующих форму и расположение проекционных поверхностей для каждого из представленных на рисунках объектов.
