Определение положения заданных точек
Аналогичным способом можно пользоваться и в тех случаях, когда необходимо определить положение каких-либо произвольно заданных точек, представленных на ортогональном чертеже (рисунок 53, в). Так, к примеру, если требуется определить перспективное местоположение точек пик, нанесенных на фасаде или же на прямой AB, равной его длине, то, как и в предыдущем примере, располагаем отрезок AB параллельно линии горизонта и проводим луч B0, определяющий положение точки W. Затем проводим из заданных точек n и k лучи в точку W, которые засекают положение этих точек на прямой AB0.
Рассмотренные выше примеры касались приемов перспективного построения плоской прямоугольной фигуры. Однако изложенные выше принципы построения распространяются и на другие случаи перспективного изображения. В частности, они имеют непосредственное отношение к построению перспективных изображений объемных фигур. Обратимся к одному из таких объектов и рассмотрим в качестве примера построение контуров здания, имеющего форму параллелепипеда. На чертеже представлены план и фасад объекта, точка зрения O, а также расположена линия горизонта на 1/4 части высоты здания, считая от основания (рисунок 54).
Особенность перспективного построения параллелепипеда выражается, прежде всего, в необходимости произвести построение не одного, как в предыдущей примере, а двух фасадов здания. В соответствии с этим при построении потребуется использовать не одну, а две проекционные поверхности для каждого фасада в дельности.
Исходя из этих условий, производим следующее построение. Проводим через точку зрения O оси X и Y, располагая их параллельно сторонам плана объекта.
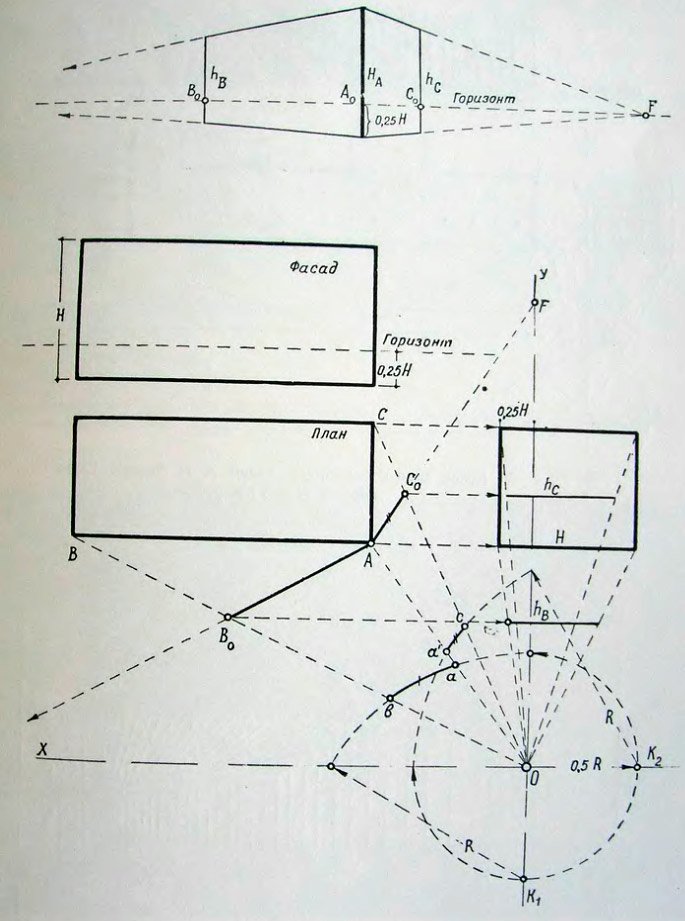
Рисунок 54. Примеры перспективного построения объекта прямоугольной формы

Рисунок 55. Новое здание библиотеки В. И. Ленина. Схема перспективного построения
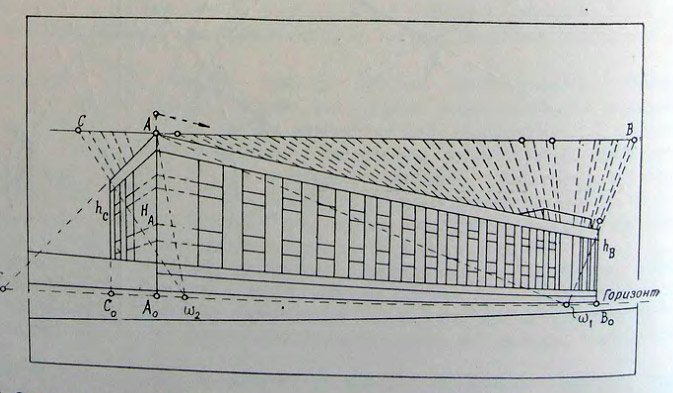
Рисунок 56. Схема перспективного изображения нового здания библиотеки имени В. И. Ленина

Рисунок 57. Перспективный вид нового здания библиотеки имени В. И. Ленина. Фотоснимок и перспектива, построенная рекомендуемым методом с той же точки зрения
Затем произвольно избранным радиусом, равным 0,5 R, из точки O вычерчиваем окружность, которая определит на осях X и Y положение центров K1 и K2 и вершины двух проекционных поверхностей. Проведя далее лучи AO, BO и CO, найдем проекции ab и a'c сторон плана на полученных поверхностях.
Расположенные изолированно, проекции эти оказываются, однако, разномасштабными, так как высота объекта H, расположенная в точке A, не получает при проекции на эти поверхности равных размеров.
Поэтому при замене этих поверхностей двумя соответственно параллельным, картинными плоскостями последние необходимо располагать таким образом, чтобы они пересекались в плане на луче, направленном к ближайшему от зрителя углу здания.
Такими плоскостями (точнее, их следами) в данном примере будут являться AB0 и AC0, точка пересечения которых в плане для удобства построения совмещена с точкой A — основанием ближнего к зрителю вертикального ребра здания.
Установив положение картинных плоскостей, переходим к построению перспективы объекта, которое осуществляется обычными приемами. Прежде всего, в верхней части рисунка проводим линию горизонта и располагаем на ней последовательно отрезки AB0, AC0 — проекции сторон плана AB и AC, а также отрезок C0F, определяющий положение точки схода F для бокового фасада параллелепипеда.
