К истории вопроса
Перспектива — это способ изображения предметов и пространства на плоскости в соответствии с теми кажущимися сокращениями размеров и изменениями очертаний окружающих тел, которые зритель наблюдает в натуре. Такое наиболее общее и в целом правильное определение перспективы можно встретить в ряде учебных пособий и в энциклопедических словарях. Это определение, с одной стороны, содержит указание на геометрическую основу данной дисциплины как способа изображения предметов на плоскости. С другой стороны, оно подчеркивает связь перспективы с законами зрения и восприятия, из которых перспектива исходит в своих научных основах.
Как средства изображения, и геометрическая перспектива и рисунок с натуры служат общей цели. С их помощью человек изображает на плоскости окружающие предметы такими, какими они представляются в пространстве. Однако пути, ведущие к достижению этой цели, для рисунка и перспективы различны. Построение перспективных изображений всегда следует строгим геометрическим системам. В рисовании же, напротив, художник руководствуется субъективными оценками и суждениями, обращаясь к геометрическим схемам лишь как к вспомогательному проверочному средству.
Строгая логика геометрических построений всегда привлекала художников и архитекторов, профессионально изучавших теорию линейной перспективы. Однако приемы перспективных построений разрабатывались вначале не как отвлеченные геометрические схемы, а как результат теоретического обобщения научных данных о зрительном восприятии. Именно так относились к теории перспективы ее создатели — художники и архитекторы эпохи Возрождения, рассматривавшие эту дисциплину как науку о зрении и зрительных лучах.
Существующий метод перспективных построений, которым мы с успехом пользуемся до настоящего времени, возник в результате обобщения крупнейших достижений изобразительной практики эпохи Возрождения. Архитектор Филиппо Бруннелеско заслуженно считается первым, установившим правила перспективы в живописи. Он построил несколько перспективных изображений на основе открытого им с помощью молодого математика Паоло Тосканелли способа получения перспективных изображений «путем пересечения». Прием этот, получивший впоследствии название метода центральной проекции предметов на плоскость, историк XVI века Вазари, так же как и современники Бруннелеско, характеризовал как «…вещь поистине в высшей степени остроумную и полезную для искусства рисования».
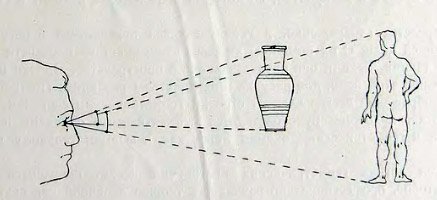
Рисунок 1. Угловые измерения перспективной величины предметов
Со времени создания этого метода прошло больше пяти столетий. Однако его принципы и геометрические основы не претерпели в течение этого периода каких-либо существенных изменений. Более того, при объяснении основ теории линейной перспективы и при освещении вопросов ее связи с практикой зрительного восприятия современный исследователь обращается, по существу, к тем же наглядным примерам и логическими рассуждениям, которыми пользовались еще ученые Возрождения несколько веков тому назад.
Каковы же эти факты и примеры, и на какие научные данные они опираются?
Как уже отмечалось выше, законы перспективы отождествлялись в эпоху Возрождения с законами зрения и восприятия. Взгляды ученых этого времени в области оптики непосредственно примыкали к древним античным и арабским традициям. Трудность объяснения перспективных явлений состояла, однако, в том, что устройство глаза не было известно. Тогда еще никто не подозревал о возможности возникновения каких-либо оптических изображений на внутренней поверхности глаза. Работу глаза представляли элементарно просто. Ученые считали, что глаз имеет отверстие — зрачок, из которого исходят или в которое проникают зрительные лучи, доносящие до зрителя «образы или подобия» объектов.
Так, например, архитектор и теоретик Леон Баттиста Альберти в своей книге «О живописи», относящейся к 30-м годам XV века и являющейся первым, дошедшим до нас письменным свидетельством, излагающим вопросы перспективы, сравнивает зрительные лучи с тончайшими нитями, распространяющимися от глаза до поверхности противолежащего предмета. Альберти писал, что проекционные размеры предметов — «видимые протяжения» — «…глаз измеряют …зрительными лучами, как ножками циркуля». «…Поэтому говорят, — продолжает он, — что при зрении образуется треугольник, основание которого — видимое протяжение, стороны же — это лучи, которые от точек протяжения тянутся до глаза …Здесь правила таковы: чем острее угол в глазу, тем видимое протяжение будет казаться меньше», и наоборот (рисунок 1).
